|
Muhammed Bin Musa El Harzemî, 780 veya 795 tarihinde Hazer Denizinin doÄŸusundaki Harzem (Aral gölünün güneyindeki bugünkü Hive) de doÄŸmuÅŸtur. DoÄŸum yerine izafeten El'Harzemî diye anılır. Harzemî beÅŸ fen dalına tesirli ÅŸekilde hizmet etmiÅŸtir.
Harzemî, matematiÄŸin geniÅŸ bir dalı olan cebirin temellerini atmıştır. Cebir mevzularını içine alan eseri, bütün dünyada cebir ilmine ad olmuÅŸtur. Harzemî, cebir bakımından Öklid'den 1000 yıl ileridedir. Cebirle ilglii meÅŸhur eserinin adı: "El'Kitab'ül-Muhtasar fi Hısab'il - Cebri ve'l-Mukabele" dir. 12 asır önce yazılan bu eser cebir sistemlerine ait kaide ve teoremler ile yeni çözüm yollarını mevzu edinir. Bu eser DoÄŸu ve Batı ilim dünyasında ilk müstakil cebir kitabı olma ÅŸerefini kazanmıştır.
El Cebr ve'l - Mukabeleyi Harzemî 830 yılında ÅŸark seyahatin dan döndüÄŸünde Halife Memun'un isteÄŸi üzerine Arapça olarak hazırlamıştır. 1145 yılında zamanın ilim dili olan Latinceye çevrilmiÅŸ ve MüsteÅŸrik F. Rosen tarafından "The Algebre Muhammed Bin Musa" adlı tercümesi 1831 yılında Arapça metni ile birlikte Londra'da yayınlanmıştır. Eser, medenî muâmelat, arazi Ölçümü, bina yapımı ve kanal hafriyatında rastlanan pratik meseleleri cebir yolu ile halle yarayacak karekterde umuma mahsus olarak kaleme alınmıştır.
Eser, bir önsöz ile beÅŸ esas bölüm ve bir de ek bölümden meydana gelmiÅŸtir. {tab=I Kısım}
Birinci Kısım: Birinci ve ikinci dereceden altı ayrı tipten denklemin (muadele) geometrik yolla çözüm metodunu ihtiva eder:
1) x2 = a, 2) x2 = bx, 3) ax = b,
4) x2 + ax = b, 5) x2 + b = ax, 6) x2 = ax + b
Bu bölümün ikinci kısmında: (a ± x) ve (b ± x) gibi "Binom Formüllerinin" çarpım kaideleri de vardır.
Ayrıca, ikinci dereceden tam olmayan üç ayrı tip denklemin (muadele) tamamen kendisine mahsus deÄŸiÅŸik çözüm yollan belirtilmiÅŸtir.
{tab=II Kısım}
Ä°kinci Kısım: Ä°kinci dereceden tam olmayan denklemlerin geometrik çözümünü mevzu edinir. Her tip denklem için iki ayrı çözüm yolu göstermiÅŸtir. Bu çözüm yollarından birincisi geometrik çözüm yolu olup, bugünkü cebirde "Kare ve dikdörtgen metodu" denmektedir. Bu çeÅŸit bir çözüm yolunu, ne eski Mısır ve Mezepotamya, ne de eski Yunan ve eski Hind matematiÄŸinde görmek mümkün deÄŸildir. Harzemî'nin bu çözüm ÅŸekli, matematikte cebir ile geometri arasında bir nevi yakınlık kurmayı hedef tutan araÅŸtırmanın ilk mahsulüdür.
{tab=III kısım}
Üçüncü Kısım: Birer terimi bilinmeyen iki terimli bir çarpanın neticesinin nasıl bulunacağını mevzu edinir. Burada, çarpanlara ayırma ve "özdeÅŸlik" nevinden hususiyetleri görmek mümkündür : (x + a) (x + b), (x + a) (x - b), (x - a) (x + b), (x — a) (x — b) ... çarpım durumlarını incelemiÅŸtir.
{tab=IV kısım} Dördüncü Kısım:  gibi iÅŸlemlerin çözüm kaidelerini ve çözüm yollarını belirtir. gibi iÅŸlemlerin çözüm kaidelerini ve çözüm yollarını belirtir. {tab=V kısım}
BeÅŸinci Kısım: Cebirle çözülebilecek bazı problemlere ayrılmıştır. Ä°ki misal verelim :
a) 10 sayısını öyle iki kısma ayırınız ki, bunların kareleri toplamı 58'e eÅŸit olsun.
b) 10 sayısını öyle Ä°ki kısma ayırınız ki bunların kareleri farkı 40 sayısına eÅŸit olsun. {tab=Son bölüm}
Eserin son ek bölümünde de; devri, için gerekli olan, amelî ve tatbikî hesaplama ÅŸekilleri, zamanın hükümet iÅŸlerine ait hesapların yapılması, kanalların açılması, bina inÅŸaatı, esnaf, tüccar ve ölçme memurları için gerekli hesapların cebirle çözüm yolları, Hint sayı iÅŸaretleri, vasiyet memurları için gerekli olan Kur'ân-ı Kerim'deki miras hukuku uygulamasını hem aritmetik hem de cebir yolu ile çözümlenecek ÅŸekilde, gerekli çözüm yollarını misalleriyle beraber gösterir.
{/tabs}
Harzemî'nin; cebir kelimesini matematiÄŸi ithâl edip, matematikte geniÅŸ bir dal olan cebiri, metodik ve sistematik hâle getiren; ikinci derece denklemlerin pozitif köklerini veren orijinal bir çözüm metodunu ilk olarak ortaya koyan; ikinci derece denklemler için, bugün "kare ve dikdörtgen metodu" denilen "grafik metodla" yani geometrik yolla çözüm yollarının, gerçekleÅŸtirilmesini cebire ilk olarak kazandıran "Kitabü'l- Cebr ve'l- Mukabele" si üzerinde bir nebze daha durarak bazı tahliller yapalım:
Cebir kelimesi Arapça'da kırık olan bir ÅŸeyi doÄŸrultmak manasına gelir. Hattâ kırık ve çıkık olan bir uzva sarılan tahtalara cebire denilir. Matematikte cebir, bir kesri tam kılma karşılığı olarak alınmıştır. Harzemî ise, cebir ve mukabele tabirini ÅŸu mânada almıştır: Cebir, bir eÅŸitliÄŸin bir tarafındaki negatif iÅŸaretli terimleri diÄŸer tarafa geçirmektir (eÅŸitliÄŸin her iki tarafında pozitif iÅŸaretli terimler kalacak ÅŸekilde). Mukabele ise, benzer terimlerin irca' ve ıslâhıdır. Meselâ: Matematik tarihinde Ömer Hayyam'ın "yaklaşık kare kök formülü" adını alan  münasebeti, münasebeti,
cebir ile  şeklini alır. şeklini alır.
Yukardaki formülün mukabelesi olmaz, çünkü benzer terimler yoktur. Hayyam'ın yukarıdaki formülü, (a + b)2 = a2 + (2a + b) b, özdeÅŸliÄŸinin yaklaşık bir ifadesi olarak aldığı anlaşılıyor.
Cebir ve Mukabelenin Birinci Kısmı baÅŸta ele aldığımız gibi, "Durûbu Sitte" veya "Mesaıl-ı Sitte" dediÄŸi altı denklemin çözüm kaidelerini isbatsız olarak ihtiva eder.
Ä°kinci Kısım, Ä°lim Tarihi bakımından en orijinal olanıdır. Bu bölümde ikinci dereceden tam olmıyan denklemlerle, aÅŸağıdaki üç tip denklemin geometrik (ki biz buna Kare ve Dik dörtgenler metodu diyeceÄŸiz) çözümlerinden bahsedilmektedir:
I. x2+Ax=B
II. x2 + B= Ax
III. x2 =Ax + B
Harzemî bilinmeyen mikdara Åžey; Åžey'in karesine Mâl; Mâl'in Åžey ile çarpımına, Kâab demiÅŸ ve bunları sırasiyle "Åž, M, K" harfleriyle göstermiÅŸtir.
Åžimdi bu kısmın meselelerini modern harf ve sembolleri kullanarak çözelim:
I. x2+Ax=B
Bu denklem için Harzemî'nin verdiÄŸi misal: Bir Mâl ile 10 Åžey' toplamının 39 dirheme eÅŸitliÄŸini temin edecek ÅŸeyin belirtilmesi yani x2+10x=39 denkleminin çözümünün tayinidir. Harzemî, yukarda-ki üç tip meselenin çözümü için ayni geometrik metodu kullanmıştır. Åžöyleki; daima mâlum farz olunan Mâl, bir kare ile temsil olunur ve verilen denklemin ÅŸartlarına (kat sayılarına) göre, Åžey' belirtilir. Harzemî verilen denklemi iki tarzda çözmüÅŸtür.

Birinci tarz: Farzedelim ki Mâl, ABCD karesiyle gösterilmiÅŸ olsun. Bu karenin kenar uzunlukları Åžey'e eÅŸit olacaktır. Åžekilde DK'yı, Åžey'in yanındaki sayı (katsayı) olan 10'un dörtte birine eÅŸit olarak (DKLC), (CMNB), (BOPA), (ARSD) gibi birbirine eÅŸit dört dikdörtgen çizelim. Bundan baÅŸka ÅŸeklîn A, B, C, D köÅŸelerinde meydana gelen dört küçük karenin alanları toplamı:  olacağı gibi, yeni meydana gelen olacağı gibi, yeni meydana gelen  karesinin alanı da 39 + 25 = 64 olur; yani bu karenin bir kenarının uzunluÄŸu 8'e eÅŸittir. Çünkü verilmiÅŸ denklem, x2 + 10 x = 39 dur. Bu neticeye göre Åžey' ile 5 sayısının toplamı 8'e eÅŸit olur. Yani x + 5 = 8 denklemi yazılır. (Çünkü karesinin alanı da 39 + 25 = 64 olur; yani bu karenin bir kenarının uzunluÄŸu 8'e eÅŸittir. Çünkü verilmiÅŸ denklem, x2 + 10 x = 39 dur. Bu neticeye göre Åžey' ile 5 sayısının toplamı 8'e eÅŸit olur. Yani x + 5 = 8 denklemi yazılır. (Çünkü  x + 5 = 8 dir). x + 5 = 8 dir).
O halde aranılan Åžey' (bilinmeyen) x = 3 tür. Bu metod gösteriyor ki Åžey'i veren formül:  dür. dür.

I. Meselenin II. Tarz Çözümü: Bu metodda Mâl yine (ABCD) karesi ve Åžey'de kenarlardan biridir. Bu sefer CK ve AE uzunluktan denklemdeki 10 kat sayısının yarısına eÅŸit alınır ve (CKJB) ile (AEFB) dikdörtgenleri teÅŸkil olunur. Buna göre ÅŸekilde taranmış alanlar toplamı x2 ile 10 x toplamına, yani 39'a eÅŸit olur ve Kare (ABCD) + 2 Dikdörtgen (BCKJ) = 39 yazılır. DiÄŸer taraftan, ÅŸeklin köÅŸesinde meydana gelen (FBJI) karesi —ki alanı 25V eÅŸittir— de taranmış alanlara ilâve edilmekte, 39 + 25 = 64 Alan (EDKI karesi) eÅŸitliÄŸe yazılır ve ED = 8 bulunmuÅŸ olur. O halde aranılan Åžey': 8 — 5=3 den ibarettir.

II. Kısım II Mesele: x2 + B = Ax denklemi: Harzemî; bu mesele için Mâl ile 21 dirhem toplamının 10 Åžey'e eÅŸit olması misalini vermiÅŸtir. (Yani, x2 + 21 = 10 x denklemi). Burada Mâl'i temsil eden kare (ABCD) olsun. Yani Åžey' = X = AB alalım. Åžimdi, bir kenarı, bilinmeyene eÅŸit farzolunun (DEFC) dikdörtgeninin alanını, denklemdeki mutlak sayı olan 21 dirheme eÅŸit alalım. Bu halde (AEFB) dikdörtgeninin alanı x2 + 21'e eÅŸit olacağından verilen x2 + 21 = 10 x denklemi kurulur. (AEFB) dikdörtgeninin bir kenarının uzunluÄŸu x olduÄŸundan diÄŸer kenarın uzunluÄŸu 10'a eÅŸittir. (Yani BF = 10 dur) Åžimdi de, BF'nin orta noktası K olmak üzere (LEMN) karesini çizelim, bu karenin alanı 25'e eÅŸittir. Bundan sonra da FP'yi AD'ye eÅŸit alıp (PFMR) dikdörtgenini teÅŸkil edelim, bunun alanının, (DLKC) dikdörtgeninin alanına eÅŸitliÄŸi aÅŸikârdır. Åžekildeki (KPRN) karesine gelince onun da alanı: 25 — 21 =4 tür. (DEFC) Alan (KLEFMRPK) = 21, ve Alan (NLEM) =25 olduÄŸundan, Alan (KPRN) = 25 - 21 = 4 olur.
Bu meselede de görülüyor ki, verilen denklemi tahkik eden 3 deÄŸeri,  formülü ile bulunmuÅŸ oluyor. (Klâsik 2. derece denklem formülünün tek iÅŸaretli hâli). formülü ile bulunmuÅŸ oluyor. (Klâsik 2. derece denklem formülünün tek iÅŸaretli hâli).

II. Kısım III. Meselesi: Bu meselede denklemin tipi X2 = AX + B dir. Harezmî'nin verdiÄŸi nümerik misal, 3 Åžey' ile 4 dirhemin bir Mâl'e eÅŸit olması, yani X2 = 3X + 4 denkleminin çözümüdür. Burada da X2 yi temsil eden ÅŸekil (ABCD) karesi ve aranılan Åžev' de AB uzunluÄŸudur. Karenin AB kenan üzerinde BK = 3 (Åžey' in katsayısı olan 3) alalım. Bu suretle teÅŸkil olunacak (KTCB) dikdörtgeninin alanı; 3X eÅŸit olacağı gibi (ADTK) dik dörtgeninin alanı da 4'e (denklemdeki mutlak sayı) eÅŸit olur, çünkü verilen denklem, 3X + 4 = X2 dir.
Åžimdi KB nin N orta noktasını iÅŸaret etmek suretiyle (KLMN) karesini çizelim, bu karenin alanı:  olur. olur.
Aynı suretle, bir kenan AN olan (ARSN) karesini teÅŸkil edelim, meydana gelen (RDTP) dik dörtgeni, (LPSM) dik dörtgenine eÅŸit olur. Çünkü, RD kenarı NB ye veya KN ye veyahut da LM'ye eÅŸittir. RP kenarı ise LP ye eÅŸittir. Çünkü her ikisi de AN-KN'ye eÅŸittir. (Åžekil 4)
O halde (ARSN) karesinin alanı, (ADTK) dikdörtgeni ile (KLMN) karesinin alanı toplamına eÅŸit olur. Bundan dolayı (ARSN) Haresinin alanı:  olacağından bunun bir kenarı olan AN de, olacağından bunun bir kenarı olan AN de,  olur. olur.
Aranılan Åžey1 AB uzunluÄŸu olduÄŸundan  eÅŸitliÄŸi bulunur. Görülüyor ki bu çizim yolu ile x bilinmeyenini vermek üzere: eÅŸitliÄŸi bulunur. Görülüyor ki bu çizim yolu ile x bilinmeyenini vermek üzere:  formülü kullanılmış demektir. formülü kullanılmış demektir.
GörüldüÄŸü gibi Harzemî ikinci derece denklemlerinin pozitif köklerini veren orjinal bir çözüm metodu bulmuÅŸtur. Çünkü kendisinden önce birçok ilim adamı bu mevzuda çalışmalar yapmıştır. Kısaca hülasa edersek: I. Hippocrates (M.Ö. 460),

denkleminin çözümünü veren geometrik bir yol göstermiÅŸtir
II. Menaechmus (MÖ. 350), X3 =k kübik denklemini, y2 = bx, xy = ab (parabol, hiperbollerin kesiÅŸtirilmesiyle çözmüÅŸtür.
III. Euclid (M.Ö. 300), x2 + ax = a ve x2 + ax = b2 denklemlerini geometrik metodla çözmüÅŸtür.
VI. Archimedes (MÖ. 215), (De Sphaera et Cylindro, Lib, II) de, küreye dair bir problemi çözerken,  orantısına veya, x3 + c2 b = cx2 kübik denklemine rastlamıştır. orantısına veya, x3 + c2 b = cx2 kübik denklemine rastlamıştır.
V. Heron (M.S. 50), 144 x (14 -x) = 6720 denklemini çözmüÅŸtür.
VI. Ä°zmirli Theon (MS. 125), x2 — 2y2 = 1, belirsiz denkleminin çözümü için bir kaide vermiÅŸtir.
VII. Diophantus (M.S. 275), x3 + x = 4x + 4 denklemini çözmüÅŸ ve bazı belirsiz ikinci derece denklemlerini (x2 —Ay2 = 1, tipinde) hal ve münakaÅŸa etmiÅŸtir.
VIII. Aryabhatta (M.S. 510), ikinci derece denklemlerinin pozitif köklerini veren formülü bulmuÅŸtur.
IX. Eutocius (M. S. 560), x3 + c2 b = cx2 denklemini
 koniklerinin kesiÅŸtirilmesi yolu ne çözmüÅŸtür. koniklerinin kesiÅŸtirilmesi yolu ne çözmüÅŸtür.
Harzemînin ise (M.S. 825) adı geçen bu meÅŸhur eserinde, Cebirde sembolizm ve ikinci derece denklemlerin çözümleri için Rönesans matematikçilerine, ikinci derece cebrine dair yapılacak büyük iÅŸler bırakmayacak kadar sistematik çalışmaları vardır. Safvet SENÄ°H |
 Matematik makaleleri
Matematik makaleleri  Cebir Ä°lmi ve Harzemi
Cebir Ä°lmi ve Harzemi 






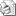
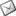
 gibi iÅŸlemlerin çözüm kaidelerini ve çözüm yollarını belirtir.
gibi iÅŸlemlerin çözüm kaidelerini ve çözüm yollarını belirtir.  münasebeti,
münasebeti, ÅŸeklini alır.
şeklini alır. 
 olacağı gibi, yeni meydana gelen
olacağı gibi, yeni meydana gelen  karesinin alanı da 39 + 25 = 64 olur; yani bu karenin bir kenarının uzunluÄŸu 8'e eÅŸittir. Çünkü verilmiÅŸ denklem, x2 + 10 x = 39 dur. Bu neticeye göre Åžey' ile 5 sayısının toplamı 8'e eÅŸit olur. Yani x + 5 = 8 denklemi yazılır. (Çünkü
karesinin alanı da 39 + 25 = 64 olur; yani bu karenin bir kenarının uzunluÄŸu 8'e eÅŸittir. Çünkü verilmiÅŸ denklem, x2 + 10 x = 39 dur. Bu neticeye göre Åžey' ile 5 sayısının toplamı 8'e eÅŸit olur. Yani x + 5 = 8 denklemi yazılır. (Çünkü  x + 5 = 8 dir).
x + 5 = 8 dir).  dür.
dür.

 formülü ile bulunmuÅŸ oluyor. (Klâsik 2. derece denklem formülünün tek iÅŸaretli hâli).
formülü ile bulunmuÅŸ oluyor. (Klâsik 2. derece denklem formülünün tek iÅŸaretli hâli).
 olur.
olur. olacağından bunun bir kenarı olan AN de,
olacağından bunun bir kenarı olan AN de,  olur.
olur. eÅŸitliÄŸi bulunur. Görülüyor ki bu çizim yolu ile x bilinmeyenini vermek üzere:
eÅŸitliÄŸi bulunur. Görülüyor ki bu çizim yolu ile x bilinmeyenini vermek üzere:  formülü kullanılmış demektir.
formülü kullanılmış demektir.
 orantısına veya, x3 + c2 b = cx2 kübik denklemine rastlamıştır.
orantısına veya, x3 + c2 b = cx2 kübik denklemine rastlamıştır. koniklerinin kesiÅŸtirilmesi yolu ne çözmüÅŸtür.
koniklerinin kesiÅŸtirilmesi yolu ne çözmüÅŸtür.