|
Bu haftaki konuÄŸumuz, hepimizin çok yakından tanıdığı, bidolu geometri kitabında yer alan sevgili ABC üçgeni. Bizimle röportaj yapmayı kabul ettiÄŸi için, özel sırlarını anlattığı için ve hepsinden öte bizim güzel sorularımıza katlandığı için teÅŸekkür ederiz. Kendisine de ettik ama, alışkanlık iÅŸte. :)
Üç kenarı bir araya getirmek için onları nasıl ikna ettiniz?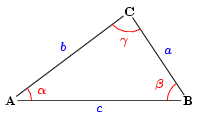
Aslında biz üçgenler için önemli olan kenarlar deÄŸil, noktalardır. Noktalar olunca onları birleÅŸtirme ÅŸansımız oluyor, böylelikle bir an da kenarlar oluveriyor. O yüzden sorunuzu deÄŸiÅŸtirmenizi isterim, lütfen biraz olsun çalışarak gelin.
Peki, özür dilerim. Noktalarınızı seçerken neye dikkat edersiniz?
Nokta seçimlerinde, cumhurbaÅŸkanlığı seçimleri kadar üzerinde durduÄŸumuz söylenemez. Bizim için üç nokta olması yeterlidir. Biz, onları rastgele seçmeye bakarız. Ama ÅŸu var ki, noktaların çakışık olup olmadığına dikkat ederiz. DoÄŸrusal olmayan üç nokta gördüÄŸümüz zaman hemen onları bir araya getirmeye bakarız.
Üçgen yapım çalışmaları nerede yapılmaktadır?
Düzlemsel bölge içerisinde çalışıp çalışmadığımız da ayrı bir önem taşır. Bundan ötürü, herhangi bir yapımda kendimizi burada buluruz.
Siz de bizim gibi açılarınızı toplar mısınız?
Evet tabi ki, yatmadan önce ve sabahları düzenli olarak toplamaya çalışırız. Tabi yok böyle bir çalışma kandırdım sizi, evet. Açılarımızın toplamı sabittir ve hiç deÄŸiÅŸmez. Ä°ç açılarımızın toplamda 180 derece eder. Dış açıların toplamı da bunun iki katıdır.
Büyük açıların karşısındaki kenar ne kadar büyüktür?
Büyük açımın karşısında her zaman büyük kenarım durur. DiÄŸerlerinden ayırt etmekte zorlandığım zamanlarda bu aklıma gelir ve karıştırmadığım için pek sevinirim.
Hani iki kenarı toplarsak, bu diÄŸer üçüncü kenarın uzunluÄŸundan büyük olur mu?
Evet, demek ki dersinize iyi çalışmışsınız. Açıkladığınız konu sahiden önemli. Herhangi iki kenarımın toplamı üçüncü kenarımdan her zaman büyüktür. Bu deÄŸiÅŸtirilemez, deÄŸiÅŸtirilmesi teklif bile edilemez.
Sevgili ABC üçgeni yıllarca ön planda oldunuz. DiÄŸer rakiplerinizin önüne geçip ÅŸöhret olmayı nasıl baÅŸardınız?
Aslında noktalara verilen harflerime borçluyum. Böylelikle ismim bütün geometri camiasına yayılmıştır.
Yani, ÅŸöhret olmak çok mu kolay?
Elbette, iÅŸinizi bilmeniz gerekir. DiÄŸer üçgenlerle aranızdaki fark sonra sonra anlaşılır, nasıl olsa.
Peki, üçgen star yarışması düzenlense kimin birinci olmasını isterdiniz?
Elbette ki, dik üçgenin olmasını isterdim. Kenarları ve açıları böylesine uyumlu olan baÅŸka bir üçgen tanımıyorum. Kaynak: Aylak Abaküs |

 Matematiksel röportajlar
Matematiksel röportajlar  ABC üçgeni ile özel röportaj
ABC üçgeni ile özel röportaj 
 Matematiksel röportajlar
Matematiksel röportajlar  ABC üçgeni ile özel röportaj
ABC üçgeni ile özel röportaj