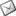
...1859 yilinda Bernhard Riemann tarafindan formülize edilmis çözülememis problemlerden biridir......Asal sayıların sıklığının;s ≠ 1 olmak kosuluyla tüm Kompleks sayilar için .......

Bu iddia ilk 1.500.000.000 çözüm için test edilmistir. Bu iddianin her çözüm için dogru oldugunun ispatlanabilmesi halinde asal sayilarin dagilimi ile ilgili çok önemli bilgiler edinmek mümkün olacaktir.

Riemann zeta hipotezi olarak da bilinmektedir, matematik alaninda ilk kez 1859 yilinda Bernhard Riemann tarafindan formülize edilmis çözülememis problemlerden biridir.

Bazi sayilarin kendilerinden küçük sayilarin çarpimi (örn. 2, 3, 5, 7, ...) cinsinden yazilamamak gibi bir özelligi vardir. Bu tür sayilara Asal sayılar denir. Asal sayilar, hem matematik hem de uygulama alanlarinda çok önemli rol oynar. Asal sayilarin tüm dogal sayilar içinde dagilimi herhangi bir örüntüyü takip etmemektedir ancak Alman matematikçi Bernhard Riemann, Asal sayıların sıklığının;s ≠ 1 olmak kosuluyla tüm Kompleks sayilar için

ζ(s) = 1 + 1/2s + 1/3s + 1/4s + ...       

biçiminde belirtilen ve Riemann Zeta Fonksiyonu olarak bilinen fonksiyonun davranisina çok bagli oldugunu gözlemledi. Riemann hipotezinin iddiasina göre ζ(s) = 0 denkleminin tüm çözümleri düz bir çizgi üzerinde yer almaktadir. Yani bu denkleminin tüm komplex çözümlerinin reel kisimlarinin 1/2 oldugu tahmin edilmektedir. Bu iddia ilk 1.500.000.000 çözüm için test edilmistir. Bu iddianin her çözüm için dogru oldugunun ispatlanabilmesi halinde asal sayilarin dagilimi ile ilgili çok önemli bilgiler edinmek mümkün olacaktir.