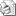
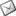
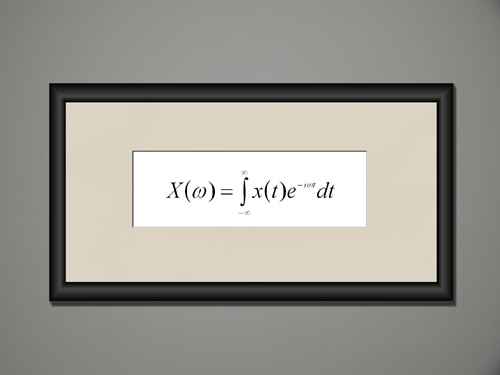
İki basit dalgayı birleştirdiğinizde yeni ve daha karmaşık bir dalga elde edersiniz. Tekrar basit bir dalga daha eklerseniz daha da karmaşık bir dalga elde edersiniz. Aslında, dalgaları birbirine ekleyerek istediğiniz karmaşıklıkta dalga elde edebilirsiniz, hatta kompleks müzik parçaları bile elde etmeniz mümkündür. 

Fakat bu işlemin tersi çok daha zordur, yani kompleks müzik parçalarının analiz etmek gerçekten zordur. Kompleks bir müzik parçasıyla başladığımızda sonunda elde edeceğimiz basit dalgaları tahmin etmek gerçekten zordur. Fakat burada matematik bizim yardımımıza yetişmektedir. Bu denklemler ne kadar karmaşık da olsa bir müzik dalgasını basit dalgalara ayırabilmektedir.

19.yy Fransız matematikçi ve mühendisi olan Joseph Fourier'in anısına bu denklem Fourier Dönüşümü olarak adlandırılmaktadır. x(t) ile ifade edilen kompleks dalgayı alır ve frekansları ? olan basit dalgalara ayırır. Bu dalgaların tamamının spektrumu x(?) ile gösterilir. ve e 2,71.. sabit sayısını, i kompleks sabiti, t zamanı, ? sonsuzluğu ? .. dt ise integrali gösterir. (integral da toplama ile ilgili matematiksel bir kavramdır)

Kaynak: JustinMullins.com'dan tercüme